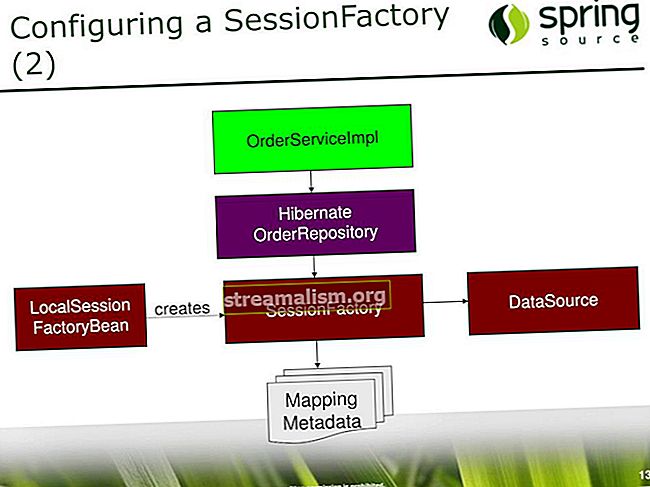
Izračunavanje n-tog korijena u Javi
1. Pregled
Pokušavajući pronaći n-ti korijen u Javi pomoću prah () je netočan u nekim slučajevima. Razlog tome je što dvostruki brojevi mogu izgubiti preciznost na putu. Stoga ćemo možda trebati polirati rezultat kako bismo riješili ove slučajeve.
2. Problem
Pretpostavimo da želimo izračunati N-ti korijen kao:
baza = 125, eksponent = 3Drugim riječima, koji je broj sa potencijom 3 125?
Pod uvjetom da n-ti korijen broja x jednak je broju x u potenciji 1 / n. Dakle, prevedemo našu jednadžbu u:
N-ti korijen = Math.pow (125, 1/3)Rezultat je 4.999999999999999. A 4.999999999999999 snage 3 nije 125. Pa kako to možemo popraviti?
3. Ispravno izračunavanje N-tog korijena
Rješenje gornjeg problema uglavnom je matematičko rješenje i vrlo je jednostavno. To je dobro poznato n-ti korijen broja x jednak je broju x u potenciji 1 / n.
Postoji nekoliko načina kako iskoristiti gornju jednadžbu. Prvo, možemo koristiti a BigDecimal i implementirati našu verziju Newton-Raphsonove metode. Drugo, možemo rezultat zaokružiti na najbliži broj i na kraju, možemo definirati granicu pogreške u kojoj će rezultati biti prihvatljivi. Usredotočit ćemo se na posljednja dva pristupa.
3.1. Krug
Sada ćemo upotrijebiti zaokruživanje kako bismo riješili svoj problem. Ponovno upotrijebimo naš prethodni primjer i vidjet ćemo kako možemo dobiti pravi rezultat:
javna praznina whenBaseIs125AndNIs3_thenNthIs5 () {double nth = Math.round (Math.pow (125, 1.0 / 3.0)); assertEquals (5, nth, 0); }3.2. Margina pogreške
Ovaj je pristup vrlo sličan gore navedenom. Samo trebamo definirati prihvatljivu marginu pogreške, pretpostavimo 0,00001:
javna praznina whenBaseIs625AndNIs4_thenNthIs5 () {double nth = Math.pow (625, 1.0 / 4.0); assertEquals (5, nth, 0,00001); }Test dokazuje da naše metode ispravno izračunavaju n-ti korijen.
4. Zaključak
Kao programeri, moramo razumjeti vrste podataka i njihovo ponašanje. Gore opisane matematičke metode djeluju jako dobro s prilično dobrom točnošću. Možete odabrati onaj koji najbolje odgovara vašem slučaju upotrebe. Kôd gornjeg rješenja nalazi se na GitHubu.