streamalism.org

1. Pregled

U ovom uputstvu prikazat ćemo algoritam za uspon na brdo i njegovu primjenu. Također ćemo se osvrnuti na njegove prednosti i nedostatke. Prije nego što izravno uskočimo u njega, razgovarajmo ukratko o algoritmu generiranja i testiranja.

2. Generiraj i testiraj algoritam

To je vrlo jednostavna tehnika koja nam omogućuje algoritmiranje pronalaska rješenja:

1. Definirajte trenutno stanje kao početno stanje
2. Primijenite bilo koju moguću operaciju na trenutno stanje i generirajte moguće rješenje
3. Usporedite novo generirano rješenje sa stanjem cilja
4. Ako je cilj postignut ili se ne mogu stvoriti nove države, prestanite. U suprotnom, vratite se na korak 2

Vrlo dobro funkcionira s jednostavnim problemima. Budući da je riječ o iscrpnoj pretrazi, nije izvedivo razmotriti je kada se radi o velikim problemima. Poznat je i kao algoritam Britanskog muzeja (pokušaj pronalaska artefakta u Britanskom muzeju slučajnim istraživanjem).

To je također glavna ideja Hill-Climbing Attack-a u svijetu biometrije. Ovaj se pristup može koristiti za generiranje sintetičkih biometrijskih podataka.

3. Uvod u jednostavni algoritam uspona na brdo

U tehnici uspona na brdo, počevši od podnožja brda, hodamo prema gore dok ne dođemo do vrha brda. Drugim riječima, započinjemo s početnim stanjem i nastavljamo poboljšavati rješenje sve dok ne postane optimalno.

To je varijacija algoritma generiranja i testiranja koji odbacuje sva stanja koja ne izgledaju obećavajuće ili izgleda da vjerojatno neće dovesti nas do ciljanog stanja. Za donošenje takvih odluka koristi se heuristikom (funkcija procjene) koja pokazuje koliko je trenutno stanje blizu ciljanog stanja.

Jednostavnim riječima, Penjanje na brdo = generiraj-i-testiraj + heuristiku

Pogledajmo algoritam jednostavnog penjanja:

1. Definirajte trenutno stanje kao početno stanje
2. Petljajte dok se ne postigne ciljno stanje ili se na trenutno stanje ne može primijeniti više operatora:
   1. Primijeni operaciju na trenutno stanje i dobiti novu državu
   2. Usporedite nova država s ciljem
   3. Prestati ako se postigne ciljno stanje
   4. Procijeniti novo stanje heurističkom funkcijom i usporedite ga sa trenutnim stanjem
   5. Ako je novije stanje bliže do cilja u odnosu na trenutno stanje, ažurirati trenutno stanje

Kao što vidimo, ciljno stanje postiže iterativnim poboljšanjima. U algoritmu uspona na brdo, pronalazak cilja je ekvivalentan dosezanju vrha brda.

4. Primjer

Algoritam uspona na brdo može se kategorizirati kao informirano pretraživanje. Tako možemo primijeniti bilo kakvu pretragu zasnovanu na čvorovima ili probleme poput problema s n-queensima koji ga koriste. Da bismo koncept lako razumjeli, uzet ćemo vrlo jednostavan primjer.

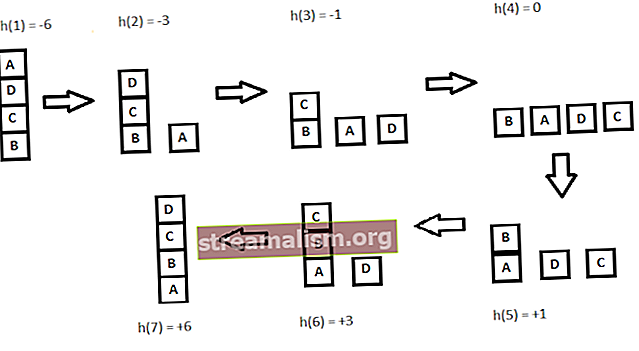
Pogledajmo sliku ispod:

Ključna točka tijekom rješavanja bilo kojeg problema uspona na brdo je odabir odgovarajuće heurističke funkcije.

Definirajmo takvu funkciju h:

h (x) = +1 za sve blokove u potpornoj strukturi ako je blok pravilno postavljen, inače -1 za sve blokove u potpornoj strukturi.

Ovdje ćemo pozvati bilo koji blok ispravno pozicioniran ako ima istu strukturu potpore kao i stanje cilja. Prema ranije spomenutom postupku uspona na brdo, pogledajmo sve iteracije i njihove heuristike kako bismo postigli ciljno stanje:

5. Provedba

Sada, implementirajmo isti primjer pomoću algoritma Hill-Climbing.

Prije svega, trebamo država klase koja će pohraniti popis stogova koji predstavljaju pozicije blokova u svakom stanju. Također će pohraniti heuristiku za to određeno stanje:

javni razred {privatni popis država; privatna int heuristika; // konstruktor kopija, postavljači i dobivači}

Također nam je potrebna metoda koja će izračunati heurističku vrijednost države.

public int getHeuristicsValue (Popis currentState, Stack goalStateStack) {Integer heuristicValue; heuristicValue = currentState.stream () .mapToInt (stack -> {return getHeuristicsValueForStack (stack, currentState, goalStateStack);}). sum (); return heuristicValue; } public int getHeuristicsValueForStack (stog stoga, popis currentState, Stack goalStateStack) {int stackHeuristics = 0; boolean isPositioneCorrect = true; int goalStartIndex = 0; za (String currentBlock: stack) {if (isPositioneCorrect && currentBlock.equals (goalStateStack.get (goalStartIndex)))) {stackHeuristics + = goalStartIndex; } else {stackHeuristics - = goalStartIndex; isPositioneCorrect = false; } goalStartIndex ++; } return stackHeuristics; } 

Nadalje, moramo definirati metode operatora koji će nam stvoriti novo stanje. Za naš primjer definirat ćemo dvije od ovih metoda:

1. Iskočite blok iz hrpe i gurnite ga na novi stog
2. Iskočite blok iz snopa i gurnite ga u jedan od ostalih snopova

private State pushElementToNewStack (Popis currentStackList, niz blokova, int currentStateHeuristics, Stack goalStateStack) {Stanje newState = null; Stog newStack = novi stog (); newStack.push (blok); currentStackList.add (newStack); int newStateHeuristics = getHeuristicsValue (currentStackList, goalStateStack); if (newStateHeuristics> currentStateHeuristics) {newState = novo stanje (currentStackList, newStateHeuristics); } else {currentStackList.remove (newStack); } vrati newState; }

private State pushElementToExistingStacks (Stack currentStack, List currentStackList, String block, int currentStateHeuristics, Stack goalStateStack) {return currentStackList.stream () .filter (stack -> stack! = currentStack) .map (stack -> {return pushElementToStack (stack, block, currentStackList, currentStateHeur; }) .filter (Objects :: nonNull) .findFirst () .orElse (null); } private State pushElementToStack (slaganje niza, niz blokova, popis currentStackList, int currentStateHeuristics, Stack goalStateStack) {stack.push (blok); int newStateHeuristics = getHeuristicsValue (currentStackList, goalStateStack); if (newStateHeuristics> currentStateHeuristics) {return new State (currentStackList, newStateHeuristics); } stack.pop (); return null; }

Sad kad imamo pomoćne metode, napišimo metodu za primjenu tehnike penjanja na brdo.

Ovdje, nastavljamo računati nove države koje su bliže ciljevima od svojih prethodnika. Stalno ih dodajemo na svom putu dok ne postignemo cilj.

Ako ne pronađemo nova stanja, algoritam se završava s porukom o pogrešci:

javni popis getRouteWithHillClimbing (Stack initStateStack, Stack goalStateStack) baca izuzetak {// instantiate initState s initStateStack // ... Popis resultPath = novi ArrayList (); resultPath.add (novo stanje (initState)); Stanje currentState = initState; boolean noStateFound = false; while (! currentState.getState (). get (0) .equals (goalStateStack) || noStateFound) {noStateFound = true; Stanje nextState = findNextState (currentState, goalStateStack); if (nextState! = null) {noStateFound = false; currentState = nextState; resultPath.add (novo stanje (nextState)); }} return resultPath; }

Uz ovo, trebamo i mi findNextState metoda koja primjenjuje sve moguće operacije na trenutnom stanju da bi se dobilo sljedeće stanje:

javno stanje findNextState (stanje currentState, Stack goalStateStack) {Popis listOfStacks = currentState.getState (); int currentStateHeuristics = currentState.getHeuristics (); vratiti listOfStacks.stream () .map (stack -> {return applyOperationsOnState (listOfStacks, stack, currentStateHeuristics, goalStateStack);}) .filter (Objects :: nonNull) .findFirst () .orElse (null); } javna država applyOperationsOnState (Popis listOfStacks, Stack stog, int currentStateHeuristics, Stack goalStateStack) {State tempState; Popis tempStackList = novi popis nizova (listOfStacks); Blok niza = stack.pop (); if (stack.size () == 0) tempStackList.remove (stog); tempState = pushElementToNewStack (tempStackList, blok, currentStateHeuristics, goalStateStack); if (tempState == null) {tempState = pushElementToExistingStacks (stack, tempStackList, block, currentStateHeuristics, goalStateStack); stack.push (blok); } vratiti tempState; }

6. Algoritam penjanja na najbrži uspon

Algoritam uspona na brzi uspon (pretraga gradijentom) varijanta je algoritma uspona na brdo. Možemo ga implementirati s malim izmjenama u našem jednostavnom algoritmu. U ovom algoritmu mi razmotriti sve moguće države iz trenutnog stanja i zatim izabrati najboljeg za nasljednika, za razliku od jednostavne tehnike penjanja na brdo.

Drugim riječima, u slučaju tehnike penjanja na brdo izabrali smo bilo koju državu kao nasljednicu koja je bliža cilju od trenutnog stanja, dok u algoritmu za penjanje na najbrži uspon odabiremo najboljeg nasljednika među svim mogućim nasljednicima i potom ažuriramo trenutno stanje.

7. Mane

Penjanje na brdo kratkovidna je tehnika jer ocjenjuje samo neposredne mogućnosti. Tako može završiti u nekoliko situacija iz kojih ne može odabrati daljnja stanja. Pogledajmo ta stanja i neka rješenja za njih:

1. Lokalni maksimum: To je država koja je bolja od svih susjeda, ali postoji bolja država koja je daleko od trenutne države; ako se lokalni maksimum dogodi unutar vidokruga rješenja, poznato je kao "podnožje"
2. Plato: U ovoj državi sve susjedne države imaju iste heurističke vrijednosti, pa je nejasno odabrati sljedeću državu lokalnom usporedbom
3. Greben: To je područje koje je više od okolnih država, ali do njega se ne može doći jednim potezom; na primjer, imamo četiri moguća smjera za istraživanje (N, E, W, S) i područje postoji u smjeru SI

Postoji nekoliko rješenja za prevladavanje ovih situacija:

1. Možemo povratak u jedno od prethodnih stanja i istražite druge smjerove
2. Možemo preskočiti nekoliko država i napraviti a skok u novim smjerovima
3. Možemo istražiti nekoliko pravaca kako bi shvatili ispravan put

8. Zaključak

Iako je tehnika penjanja na brdo puno bolja od iscrpne pretrage, još uvijek nije optimalna u velikim problematičnim prostorima.

Uvijek možemo kodirati globalne informacije u heurističke funkcije kako bismo donosili pametnije odluke, ali tada će računska složenost biti puno veća nego što je bila ranije.

Algoritam penjanja na brdo može biti vrlo koristan ako se udružite drugim tehnikama. Kao i uvijek, cjelovit kod za sve primjere možete pronaći na GitHubu.