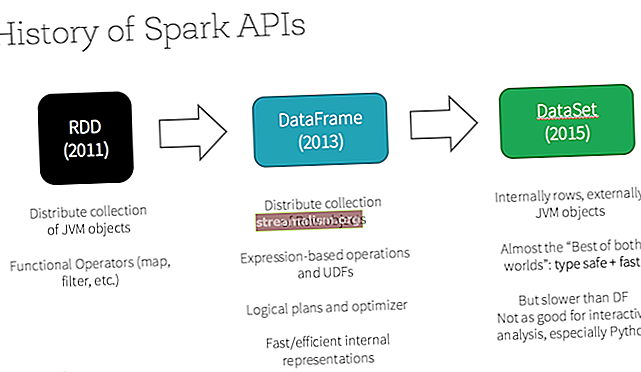
Sortiranje odabira na Javi
1. Uvod
U ovom uputstvu ćemo nauči Sortiranje odabira, pogledajte njegovu implementaciju u Javi i analizirajte njezinu izvedbu.
2. Pregled algoritma
Sortiranje odabira započinje elementom na 1. položaju nerazvrstani niz i skenira kroz sljedeće elemente u pronaći najmanji element. Jednom pronađen, najmanji element zamijenjen je elementom na 1. mjestu.
Algoritam se zatim prebacuje na element na 2. položaju i pregledava sljedeće elemente kako bi pronašao indeks 2. najmanjeg elementa. Jednom pronađen, drugi najmanji element zamijenjen je elementom u 2. položaju.
Taj se postupak odvija dok ne dođemo do n-1-og elementa niza, koji n-1-i najmanji element stavlja na n-1-i položaj. Posljednji element automatski pada na mjesto, u n-1-oj iteraciji, sortirajući tako niz.
Pronašli smo najveći element umjesto najmanjeg elementa za sortiranje niza u opadajućem redoslijedu.
Pogledajmo primjer nesortiranog niza i razvrstajmo ga uzlazno kako bismo vizualno razumjeli algoritam.
2.1. Primjer
Razmotrite sljedeći nerazvrstani niz:
int [] arr = {5, 4, 1, 6, 2}
Ponavljanje 1
Uzimajući u obzir gore navedeni rad algoritma, započinjemo s elementom na 1. položaju - 5 - i pretražujemo sve sljedeće elemente kako bismo pronašli najmanji element - 1. Zatim zamijenimo najmanji element s elementom na 1. položaju.
Izmijenjeni niz nows izgleda ovako:
{ 1 , 4 , 5 , 6 , 2 }
Ukupno izvršenih usporedbi: 4
Ponavljanje 2
U drugoj iteraciji prelazimo na 2. element - 4 - i pretražujemo sljedeće elemente kako bismo pronašli drugi najmanji element - 2. Zatim zamijenimo drugi najmanji element s elementom na 2. položaju.
Izmijenjeni niz sada izgleda ovako:
{ 1 , 2 , 5 , 6 , 4 }
Ukupno izvršenih usporedbi: 3
Nastavljajući slično, imamo sljedeće ponavljanja:
Ponavljanje 3
{ 1 , 2 , 4 , 6 , 5 }
Ukupno izvršenih usporedbi: 2
Ponavljanje 4
{ 1 , 2 , 4 , 5 , 6 }
Ukupno izvršenih usporedbi: 1
3.Provedba
Primijenimo Sortiranje odabira pomoću nekoliko za petlje:
javna statička void sortAscending (final int [] arr) {for (int i = 0; i <arr.length - 1; i ++) {int minElementIndex = i; za (int j = i + 1; j arr [j]) {minElementIndex = j; }} if (minElementIndex! = i) {int temp = arr [i]; arr [i] = arr [minElementIndex]; arr [minElementIndex] = temp; }}}Naravno, da bismo to preokrenuli, mogli bismo napraviti nešto sasvim slično:
javna statička praznina sortDescending (final int [] arr) {for (int i = 0; i <arr.length - 1; i ++) {int maxElementIndex = i; for (int j = i + 1; j <arr.length; j ++) {if (arr [maxElementIndex] <arr [j]) {maxElementIndex = j; }} if (maxElementIndex! = i) {int temp = arr [i]; arr [i] = arr [maxElementIndex]; arr [maxElementIndex] = temp; }}}I s malo više masti za laktove, mogli bismo ih kombinirati pomoću Usporedniks.
4. Pregled izvedbe
4.1. Vrijeme
U primjeru koji smo vidjeli ranije, za odabir najmanjeg elementa potrebno je ukupno (n-1) usporedbe nakon čega je zamijenjena na 1. poziciju. Slično tome, odabir sljedećeg najmanjeg potrebnog elementa (n-2) usporedbe nakon kojih slijedi zamjena na 2. mjestu itd.
Dakle, počevši od indeksa 0, izvodimo n-1, n-2, n-3, n-4…. 1 usporedbe. Posljednji element automatski dolazi na mjesto zbog prethodnih ponavljanja i zamjena.
Matematički, zbroj prvog n-1 prirodni brojevi reći će nam koliko usporedbi trebamo da bismo sortirali niz veličina n pomoću Sortiranja odabira.
Formula za zbroj n prirodni brojevi je n (n + 1) / 2.
U našem slučaju trebamo zbroj prvih n-1 prirodni brojevi. Stoga zamjenjujemo n s n-1 u gornjoj formuli dobiti:
(n-1) (n-1 + 1) / 2 = (n-1) n / 2 = (n ^ 2-n) / 2
Kao n ^ 2 izraženo raste kao n raste, smatramo višom snagom n kao mjerilo performansi, čineći ovaj algoritam a vremenska složenost O (n ^ 2).
4.2. Prostor
Što se tiče složenosti pomoćnog prostora, Sortiranje odabira zahtijeva jednu dodatnu varijablu koja privremeno drži vrijednost za zamjenu. Stoga, Sortiranje odabira složenost prostora je O (1).
5. Zaključak
Sortiranje odabira vrlo je jednostavan algoritam sortiranja za razumijevanje i primjenu. Nažalost, Njegova kvadratna vremenska složenost čini je skupom tehnikom sortiranja. Također, budući da algoritam mora skenirati svaki element, složenost najboljeg slučaja, prosječnog slučaja i najgoreg slučaja je ista.
Druge tehnike sortiranja poput Insertion Sort i Shell Sort također imaju kvadratnu vremensku složenost u najgorem slučaju, ali imaju bolju izvedbu u najboljim i prosječnim slučajevima.
Pogledajte cjeloviti kod za Sortiranje odabira na GitHubu.